cas/taxonomy/field.php (field)

Urban Modeling
Cellular Automata & Agent-Based Models offer city simulations whose behaviors we learn from. What are the strengths & weaknesses of this mode of engaging urban complexity?
There is a large body of research that employs computational techniques - in particular agent based modeling (ABM) and cellular automata (CA) to understand complex urban dynamics. This strategy looks at how rule based systems yield emergent structures.
Creating computer models is one of the most common ways to integrate complexity ideas into many fields - so much so that this methodological approach is often confused with the domain of knowledge itself. This is largely the case in urban discourses, where the construction of simulation models - either agent-based or cellular automata - is perhaps the most frequently employed strategy to try to grapple with complexity (though other communicative and relational approaches in planning have recently been gaining increased traction). It is therefore important to understand how these models work, and what aspects of complexity they highlight.
Cellular Automata
Early investigations as to the dynamics underlying complex systems came via early computational models, which illustrated how simple program rules could produce unexpectedly rich (or complex) results. John Conway's Game of Life (from 1970) was amongst the first of these models, composed of computer cells on a three dimensional lattice that could either be in an 'on' or 'off' mode. An initial random state launches the model, after which each cell updates its status depending on the state of directly neighboring cells (the model is described in detail under Bottom-up Agents). Conway was able to demonstrate that, despite the simplicity of the model rules, unexpected explosions of pattern and emergent orders were produced as the model proceeded through ongoing iterations.
At around the same time, Economist Thomas Schelling developed his segregation model, using a cellular lattice to explore the amount of bias it would require for "neighborhoods" of cells to become increasingly segregated. Cities in the US, in particular, had been experiencing the physical segregation of cities by race, with the assumption being that such spatial divisions were the result of strong biases amongst residents. With his model, Shelling demonstrated that, in effect, total segregation could occur even when agent 'rules' were only slightly biased towards maintaining neighborhood homogeneity. While the model does not explain why spatial segregation occurs in real-world settings, it does shed light on the idea that strong racial preferences are not, by necessity, the only reason why spatial partitioning may occur.
Because of the implicitly spatial qualities of models like Conway's and Shelling's, both computer programmers and urban thinkers began to wonder if models might help explain the kinds of spatial and formal patterns seen in urban development. If so, then by testing different rule sets one might be able to predict how iterative, distributed (or bottom-up) decision-making ultimately affects city form.
This is a unique direction for planning, in that most urban strategies focus on generating broad, top-down master-plans, where the details are ultimately filled in at a lower level. Here, the strategy is inverted. Models place decision-making at the level of the individual cell in a lattice, and it is through interacting populations of these cells that some form of organization is achieved. Models were able to demonstrate that, depending on the nature of the interaction rules, the formal characteristics of this emergent order can differ dramatically.
Ultimately, by running multiple models, and observing what kinds of rule-sets generate particular, recurrent kinds of pattern and form, modelers are able to speculate on what policy-decisions around planning are most likely to achieve forms deemed 'desirable' (on the assumption that the models are capturing the most salient feature of the real world conditions, which is not always the easiest assumption to make!).
Agent Based Models
Cellular Automata simulations are formulated within a lattice-type framework, but clearly this has its limits. The assumption of the model is that populations of cells within the lattice have inter-changeable rule sets, and that emergent features are derived from interactions amongst these identical populations. Clearly the range of players within a real-world urban context are quite variable, and populations of uniformly behaving cells do not capture this variance. Accordingly, with the growth in computing power, a new kind of "agent-based model" was able to liberate cells (or agents) from their lattices, as well as enabling programmers to provide differing rule-sets for multiple, differing agents.
In such models, we might have two sets of agents, (predator/prey), or agents moving in a non-static environments (flocking birds/schools of fish). Simple rules sets are then tested and calibrated to see if behaviors emerge within the models that emulate real-world observations. These models then demonstrate how different populations of actors or 'agents' with differing goals and rule sets interact.
Models that are straightforward to code (Net Logo is a good example, which can be deployed either as a CA or an Agent-Based model), showcase how different populations/agents within a model interact, producing unexpected results. Rules of interaction can be easily varied, according to a limited number of defined parameters.
That said, depending on how variables are calibrated, very different kinds of global behaviors or patterns emerge.
Urban Applications:
All of this is of great interest to urban computational geographers, who attempt to employ computer models as stand-ins for real world situations. From an urban standpoint, an agent might be a resident, a business owner, a shop-keeper, etc. Depending on the rules for growth, purchase pricing, development restrictions, or formal (physical) attributes, these agents can be programmed to interact upon an urban field, with multiple urban simulations (that use the same rule sets), serving to probe the 'field of possibilities' to see if any regularities emerge across different scenarios or iterations. If such patterns are observed, then the rules can be altered - in an attempt to derive which rule characteristics are the most salient in terms of generating either favorable or unfavorable spatial conditions (again, with the proviso that the interpretation of 'favorability' might well be contested).
Such models, for example, might attempt to show the impact of a new roadway on traffic patterns, with various rules around time, destination, starting position, etc. By running various tests of road locations, a modeler might attempt to determine the 'best' location for a new road - with the 'fitness' of this selection tying in to pre-determined policy parameters, such as land costs associated with location, reduction of congestion/travel times, or other factors. The promise of these models is very powerful: to simulate real-world conditions within a computer and then build multiple test 'worlds' prior to real-life implementation. This allows modelers to minimize policy risk of unknown consequences that are teased out in simulations.
Inherent Risks
That said, in practice there is always the concern of what models do not include: are the assumptions of the model in fact in alignment with the real world? To alleviate this, modelers attempt to calibrate their models to real world conditions by using data sets wherever possible, but they remain limited by which data types are available to them. Furthermore, the fact that a given data-set is available for use/calibration purposes, does not necessarily mean that the features the data captures are in fact related to the most salient indicators or features of the real-world system.
Models, can often be seen as 'objective' or 'scientific', since once the code has been written, the models provide reliable, quantitative results, but this does not mean that the consistency of the model is consistent with the real-world conditions being model. The model is still subject to the biases of the coding, the decisions of the modeler, and ideas around what to include and what to disregard as unimportant.
In an effort to include more and more potential factors (and again, with rising computer power) agent-based models have become increasingly sophisticated, integrating additional real-world conditions. However, as the models grow to contain more and more conditions, actors, and rules, their relationship to complex adaptive systems perspectives has become increasingly tenuous. Scientists originally interested in the dynamics of complex systems were struck by the fact that simple systems with simple rules could generate complex orders. It should not, however, be surprising that complex models, with increasingly complex rule sets can generate complex orders, but the effort going into the creation of such models, their calibration, and their interpretation (in terms of how they guide policy), seems to have moved increasingly far away from the underpinnings of their inspiration.
What seems to have been preserved from complexity theory - rather than the simplicity of complex systems dynamics - are three ideas: that of "bottom-up" rather than top-down logic - whereby the order of the system emerges without need for top down control, and the idea of "emergence": that interacting agents within the model can generate novel global patterns or behaviors that have not been explicitly programmed into the system. Finally, at the individual agent level, the rules can still retain a simplicity.
While many individual researchers and research clusters investigate urban form through modeling, it is worth making special note of CASA - The Center for Advanced Spatial Analysis at the Bartlett in London, a group led by Professor Mike Batty.
Model Attributes: Fractals and Power Laws
Of interest to Urban Modelers is not just the emergent patterns found in simulations, but also the ways in which these patterns correspond to features associated with complex systems. For example, many models display Fractals qualities. The illustration below (taken from an article by Mike Batty) show variants of how CA rules generate settlement decisions, with fractal patterns emerging in each case. Different initial conditions/constraints yield different kinds of fractal behavior (except in starting condition B).

Example of Emergent Fractal spatial characteristics, 'A digital breeder for designing cities' (2009)
Similarly, models often exhibit Power Laws in their emergent characteristics - whether this be factors such as population distributions of cities in a model, or distributions of various physical attributes within a given city. For example, an analysis of internal city road networks might reveal that road use frequency in a given city follows a power-law distribution; another analysis might reveal that cities within a given country can be ordered by size, and that populations between cities follow a power law distribution (this characteristic seems to hold for cities that together form part of a relatively interdependent network - for example the grouping of all cities in the USA, or France, but not groupings of all cities in the world, suggesting that these are not part of the same system).
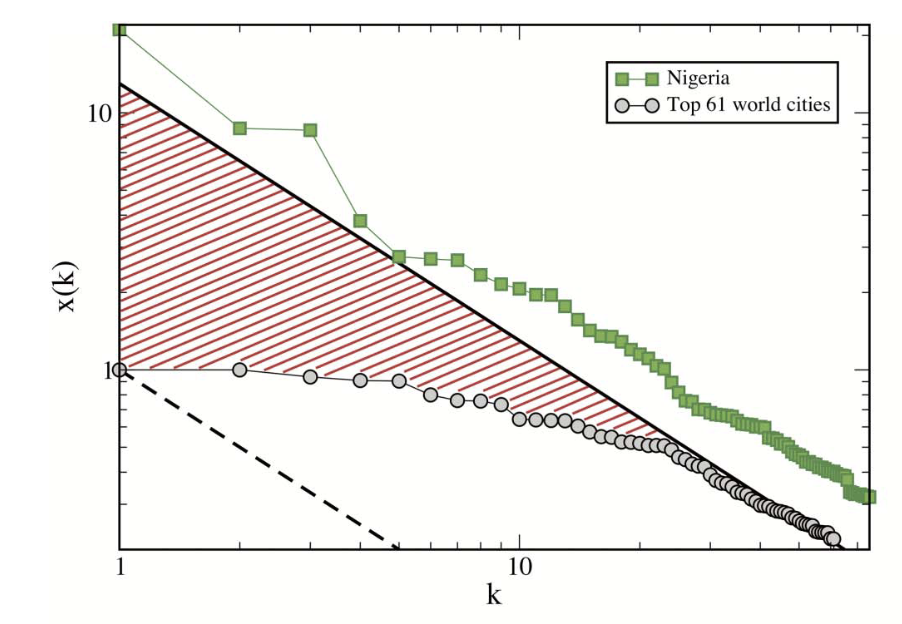
Example of power-law distribution of city populations in Nigeria, which closely follow Zipf's law: Image from Scientific Report "There is More than a Power Law in Zipf" by Cristelli, Batty and Pietronero (2012)
Many academic papers from the urban modeling world stress these attributes, which are not planned for and which are often characterized as being the 'fingerprint of complexity'.
Model Dynamics: Tipping Points & Contingency
Alongside these observed attributes of models - power laws and fractals - modelers are also interested in how models unfold over time. One of the interesting aspects of models is that, while the overall characteristics of emergent features might be similar across different models, the specificity of these characteristics will vary.
For example, a model might wish to consider locational choices of individual within a region, and including populations of agents that include such categories as: 'job opportunities', 'job seekers', and 'land rent rates'. In such a scenario, what begins as a neutral lattice of agent populations will ultimately begin to partition and differentiate with varying areas of population intensity (cities, towns) emerging. The size of these various populations centers might then follow a power-law. If we repeat the simulation with the same rules in place, we would expect to see similar power-law population patterns emerge, but the specificity of exactly where these centers are located is contingent - varying from simulation to simulation.
This raises the question of the true nature of cities and population dynamics: for example, the fact that Chicago is a larger urban hub than St. Louis might be taken as a given - the result of some 'natural' advantage that St Louis does not have. But model simulations might suggest otherwise - that the emergence of Chicago as the major mid-west hub is a contingent, emergent phenomena: and that history could have played out differently.
Models therefore allow geographers to understand alternative histories, and consider how what might seems like a 'natural' outcome, seen as part of a clear causal chain, are in fact much more tenuous and contingent phenomena. Had the rules playing out just a little differently, from a slightly different starting point, a completely different result might have ensured. Here, we are left with the realization that History Matters, and that Contingency plays a key role in the make-up of our lived world.
Another way this can be thought of is the idea of a Tipping Points: that whether or not Chicago or St Louis became a major urban center was the result of a small variable that pushed the system towards one regime, whereas another, but completely different regime was equally viable.
Tipping Points are discussed elsewhere on this site, but it is important to state that they can be thought of in two different ways: the first is this idea of a minor fluctuation that launches a given system along one particular path versus another, due to reinforcing feedback. The second looks at how an incremental increase in the stress or input to a system, once moved beyond a certain threshold, can push a system into an entirely new form of behavior.
This second idea becomes important in modeling the amount of stress or inputs a given urban system can tolerate (or absorb) before one behavioral regime shifts to another. For example incrementally rising fuel prices might reach a point where people opt to take public transit. Or a certain critical mass of successful business ventures might eventually result in a new neighborhood hub, at which point rents increase substantially. What is interesting about these points is that the shift is often abrupt, as people recalibrate their expectations and behaviors around a new set of parameters that have exceeded a particular threshold. Models can display these abrupt shifts, or Phase Transitions, where certain patterns disappear only to be replaced by others.
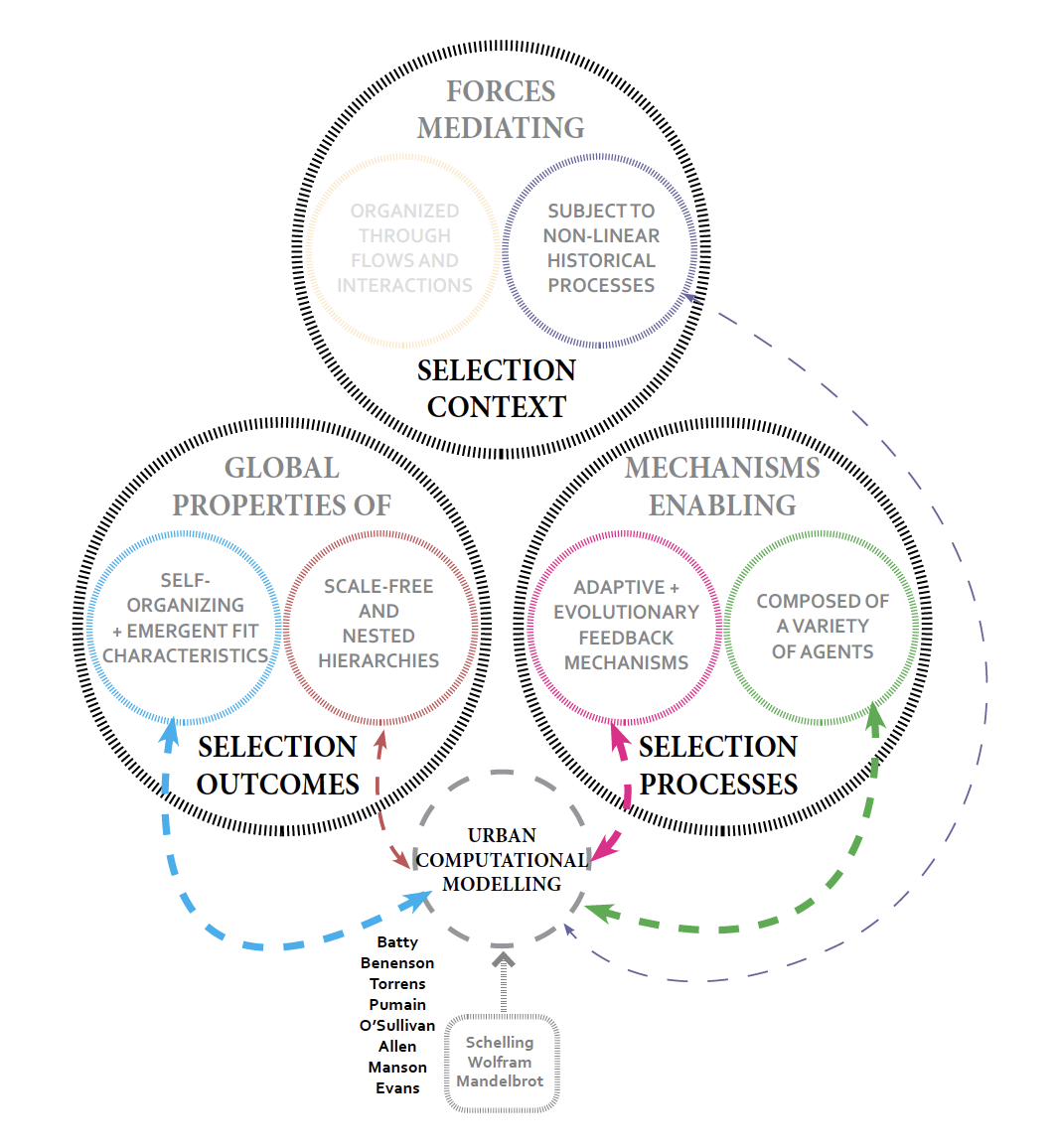
A sketch outlining some of the ideas and individuals associated with urban modeling
Back to Complexity & Urbanism
Back to Navigating Complexity
Photo Credit and Caption: markus_spiske_uPXs5Vx5bIg_unsplash.jpg
Cite this page:
Wohl, S. (2022, 8 June). Urban Modeling. Retrieved from https://kapalicarsi.wittmeyer.io/field/urban-computational-modeling
Urban Modeling was updated June 8th, 2022.
Nothing over here yet
This is the feed, a series of related links and resources. Add a link to the feed →
Nothing in the feed...yet.
This is a list of People that Urban Modeling is related to.
Segregation model
Economist who developed one of the first cellular automata demonstrations: showing how segregation of agents will emerge as a phenomena due to simple rules that, in and of themselves, do not appear to be strongly linked to segregation outcomes.
Learn more →Urban Modeling
Peter Allen is a Professor in the field of complexity and system theory, often relating his work to architecture and urban design.
Learn more →Urban Computational Modeling
Mike Batty is one of the key contributors to modeling cities as Complex Adaptive Systems
Learn more →
City Scaling
This is a default subtitle for this page. Learn more →Game of Life
This is a default subtitle for this page. Learn more →This is a list of Terms that Urban Modeling is related to.
For a system to adapt, it needs to have variables to adjust.
See also: Requisite Variety
Learn more →The idea that systems can have more than one stable state.
Early versions of systems theory assumed that systems could be 'optimized' to a single condition. CAS analysis assumes that more than one system state can satisfy optimizing criteria, and so the system is able to gravitate to multiple equilibria.
Learn more →Agents in a Complex System are guided by neighboring agents - nonetheless leading to global order.
More coming soon!
Learn more →Building blocks form the foundation of larger scale patterns within Complex Systems.
The nature of a building block varies according to the system: it may take the form of an ant, a cell, a neuron or a building.
Learn more →Complex systems do not follow linear, predictable chains of cause and effect. Instead, system trajectories can diverge into wildly different regimes. The moment when a complex system move from one trajectory to another is known as a system bifurcation.
This feature of complex systems means that the behavior of a system cannot be known in advance, but instead needs to be enacted in time. Learn more →This is a list of Urban Fields that Urban Modeling is related to.
This is a list of Key Concepts that Urban Modeling is related to.
Complex systems are composed of agents governed by simple input/output rules that determine their behaviors.
One of the intriguing characteristics of complex systems is that highly sophisticated emergent phenomena can be generated by seemingly simple agents. These agents follow very simple rules - with dramatic results.
Learn more →Complex System behaviors often exhibit power-laws: with a small number of system features wielding a large amount of system impact.
Power laws are particular mathematical distributions that appear in contexts where a very small number of system events or entities exist that, while rare, are highly impactful, alongside of a very large number of system events or entities exist that, while plentiful, have very little impact. Learn more →
CAS systems unfold over time, with agents continuously adjusting behaviors in response to feedback. Each iteration moves the system towards more coordinated, complex behaviors.
The concept of interactive, incremental shifts in a system might seem innocent - but with enough agents and enough increments we are able to tap into something incredibly powerful. Evolutionary change proceeds in incremental steps - and with enough of these steps, accompanied by feedback at each step, we can achieve fit outcomes. Any strategies for increasing the frequency of these iterations will further drive the effectiveness of this iterative search.
Learn more →Complex Adaptive Systems become more 'fit' over time. Depending on the system, Fitness can take many forms, but all involve states that achieve more while expending less energy.
What do we mean when we speak of Fitness? For ants, fitness might be discovering a source of food that is abundant and easy to reach. For a city, fitness might be moving the maximum number of people in the minimum amount of time. But fitness criteria can also vary - what might be fit for one agent isn't necessarily fit for all.
Learn more →
Feedback loops occur in system where an environmental input guides system behavior, but the system behavior (the output), in turn alters the environmental context.
This coupling between input affecting output - thereby affecting input - creates unique dynamics and interdependencies between the two.
Learn more →Complex Systems can unfold in multiple trajectories. However, there may be trajectories that are more stable or 'fit'. Such states are considered 'attractor states'.
Complex Adaptive Systems do not obey predictable, linear trajectories. They are "Sensitive to Initial Conditions", such that small changes in these conditions can lead the system to unfold in unexpected ways. That said, in some systems, particular 'potential unfoldings' are more likely to occur than others. We can think of these as 'attractor states' to which a system will tend to gravitate.
Learn more →Navigating Complexity © 2015-2025 Sharon Wohl, all rights reserved. Developed by Sean Wittmeyer
Sign In (SSO) | Sign In
Related (this page): Non-Linearity (26), Nested Orders (23), LINKS (56), Emergence (24), Bottom-up Agents (22), Variables (58), Scale-Free (217), Rules (213), Multiple Equilibria (79), Local Interactions (89), Iterations (56), Feedback (88), Building Blocks (63), Bifurcations (81), Attractor States (72),
Section: fields
Non-Linearity Related (same section): Urban Modeling (11, fields), Resilient Urbanism (14, fields), Relational Geography (19, fields), Landscape Urbanism (15, fields), Evolutionary Geography (12, fields), Communicative Planning (18, fields), Assemblage Geography (20, fields), Related (all): Tipping Points (218, concepts), Path Dependency (93, concepts), Far From Equilibrium (212, concepts),
Nested Orders Related (same section): Urban Modeling (11, fields), Urban Informalities (16, fields), Resilient Urbanism (14, fields), Related (all): Self-Organized Criticality (64, concepts), Scale-Free (217, concepts), Power Laws (66, concepts),
Emergence Related (same section): Urban Modeling (11, fields), Urban Informalities (16, fields), Urban Datascapes (28, fields), Incremental Urbanism (13, fields), Evolutionary Geography (12, fields), Communicative Planning (18, fields), Assemblage Geography (20, fields), Related (all): Self-Organization (214, concepts), Fitness (59, concepts), Attractor States (72, concepts),
Driving Flows Related (same section): Urban Datascapes (28, fields), Tactical Urbanism (17, fields), Relational Geography (19, fields), Parametric Urbanism (10, fields), Landscape Urbanism (15, fields), Evolutionary Geography (12, fields), Communicative Planning (18, fields), Assemblage Geography (20, fields), Related (all): Open / Dissipative (84, concepts), Networks (75, concepts), Information (73, concepts),
Bottom-up Agents Related (same section): Urban Modeling (11, fields), Urban Informalities (16, fields), Resilient Urbanism (14, fields), Parametric Urbanism (10, fields), Incremental Urbanism (13, fields), Evolutionary Geography (12, fields), Communicative Planning (18, fields), Related (all): Rules (213, concepts), Iterations (56, concepts),
Adaptive Capacity Related (same section): Urban Modeling (11, fields), Urban Informalities (16, fields), Tactical Urbanism (17, fields), Parametric Urbanism (10, fields), Landscape Urbanism (15, fields), Incremental Urbanism (13, fields), Evolutionary Geography (12, fields), Related (all): Feedback (88, concepts), Degrees of Freedom (78, concepts),
