Scale-Free

A good example here is the fractal features of a leaf:

We can think of the capillary network as the minimum structure required to reach the maximum surface area.

Nature's Optimizing Algorithm

Here, the scale-free structure of the capillary network allows the most efficient transport of nutrients to all parts of the leaf surface within the overall shortest capillary path length. This 'shortest overall path length'  is one of the reasons that we might often see scale-free features in nature: this may well be the natural outcome of nature 'solving' the problem of how to best economize flow networks.

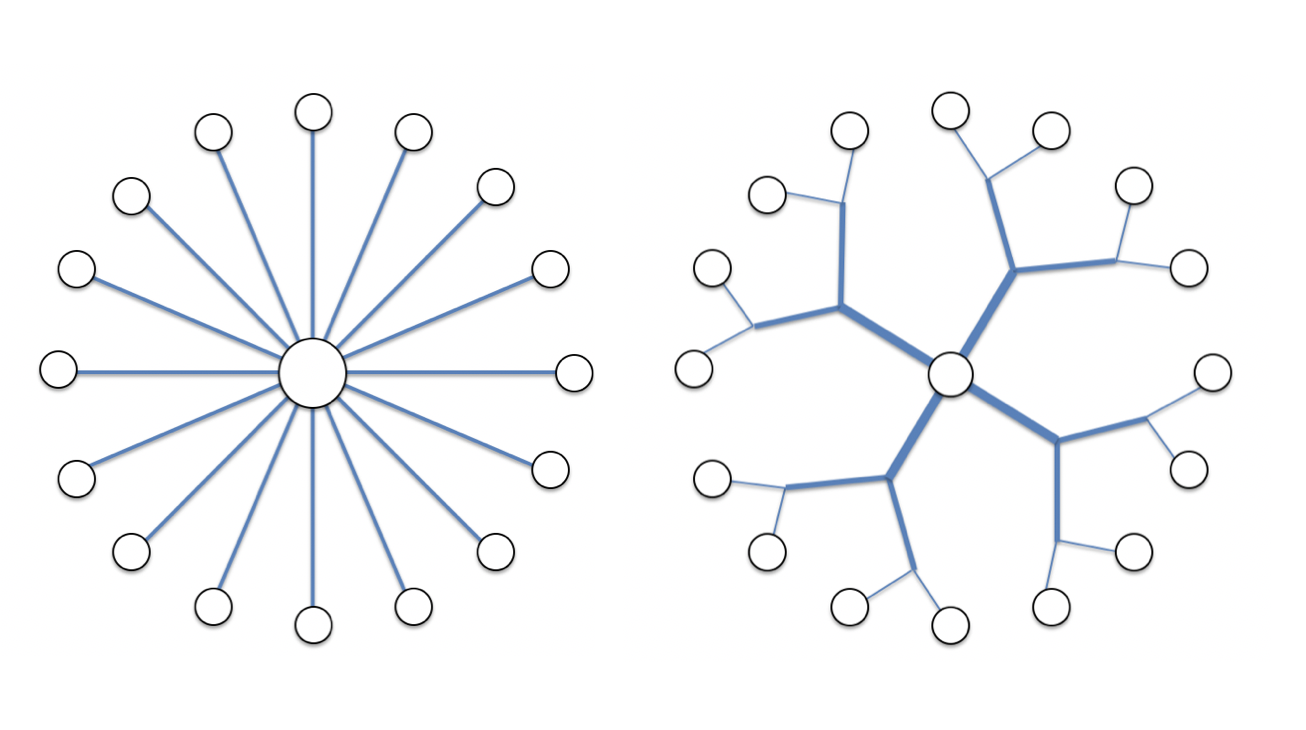
minimum global path length to reach all nodes

The two images serve to illustrate the idea of shortest overall path length. If we wish to get resources from a central node to 16 nodes distributed along a surrounding boundary, we can either trace a direct path to each point from the center, or we can partition the path into splitting segments that gradually work their way towards the boundary. While each individual pathway from the center to an individual node is longer in the right hand image, the total aggregate of all pathways to reach all nodes from the center is shorter. Thus the image on the right (which shows scale-free characteristics), is the more efficient delivery network.

Example - Street Networks:

We should therefore expect to see such forms of scale-free dynamics in other non-natural systems that carry and distribute flows: thus, if we think of size distribution of road networks in a city, we would expect a small number of key expressways carrying large traffic flows, followed by a moderate number of mid-scaled arteries carrying mid-scale flows, then a large number of neighborhood streets carrying moderate flows, and finally a very high number of extremely small alleys and roads that each carry very small flows to their respective destinations.

mud fractals and street networks

Fractals, scale-free networks, self-similar entities and power-law distributions are concepts that can be difficult to disambiguate. Not all scale-free networks look like fractals, but all fractals and scale-free networks follow power-laws. Finally, there are many power-law distributions that neither 'look' like fractals, nor follow scale-free network characteristics: if we take a frozen potato and smash it on the ground, then classify the size of each piece, we would find that the distribution of smashed potato pieces follows a power law (but is not nearly as pretty as a fractal!). Finally, self-similar entities (like the romanesco broccoli shown below) are fractal-like (you can zoom in and see similar structure at different scales), but are not as mathematically precise as a fractal.

credit: Wikimedia commons  (Jon Sullivan)

Back to Core Concepts

Back to Navigating Complexity

Photo Credit and Caption: Underwater image of fish in Moofushi Kandu, Maldives, by Bruno de Giusti (via Wikimedia Commons)

Cite this page:

Wohl, S. (2022, 30 May). Scale-Free. Retrieved from https://kapalicarsi.wittmeyer.io/definition/scale-free

Scale-Free was updated May 30th, 2022.