Creating computer models is one of the most common ways to integrate complexity ideas into many fields - so much so that this methodological approach is often confused with the domain of knowledge itself. This is largely the case in urban discourses, where the construction of simulation models - either agent-based or cellular automata - is perhaps the most frequently employed strategy to try to grapple with complexity (though other communicative and relational approaches in planning have recently been gaining increased traction). It is therefore important to understand how these models work, and what aspects of complexity they highlight.
Cellular Automata
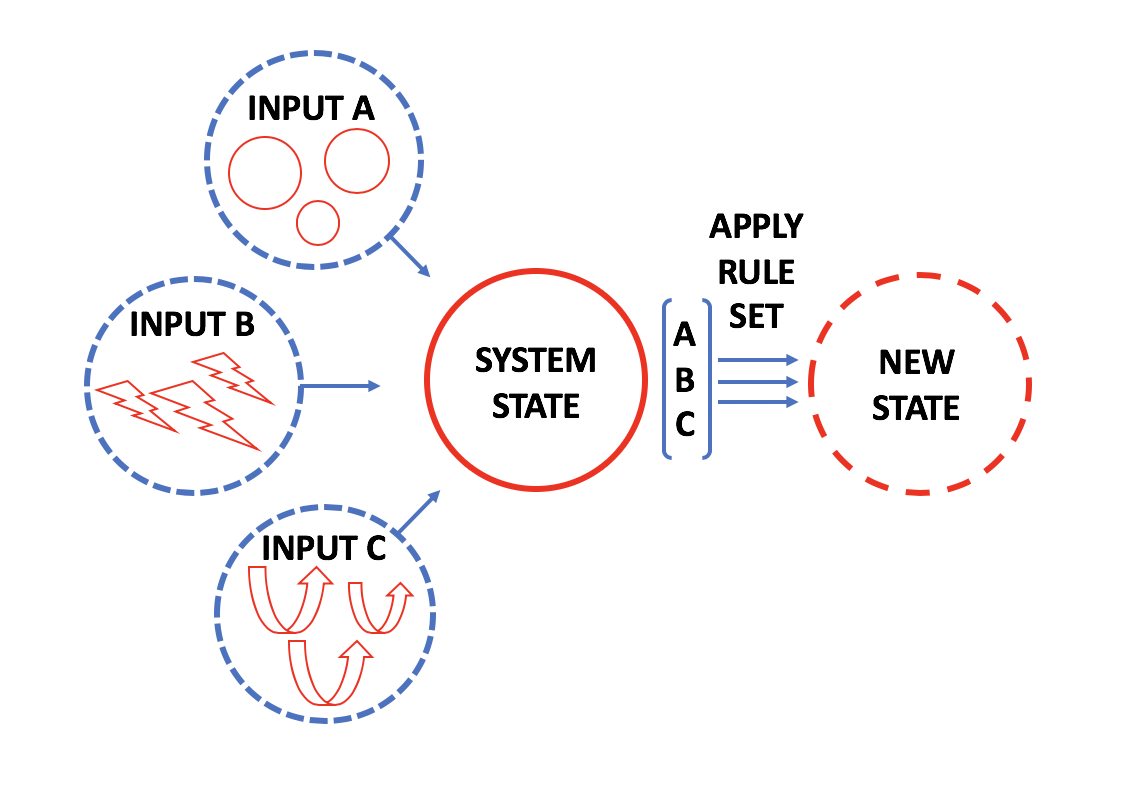
Early investigations as to the dynamics underlying complex systems came via early computational models, which illustrated how simple program rules could produce unexpectedly rich (or complex) results. John Conway's Game of Life (from 1970) was amongst the first of these models, composed of computer cells on a three dimensional lattice that could either be in an 'on' or 'off' mode. An initial random state launches the model, after which each cell updates its status depending on the state of directly neighboring cells (the model is described in detail under Bottom-up Agents). Conway was able to demonstrate that, despite the simplicity of the model rules, unexpected explosions of pattern and emergent orders were produced as the model proceeded through ongoing iterations.
At around the same time, Economist Thomas Schelling developed his segregation model, using a cellular lattice to explore the amount of bias it would require for "neighborhoods" of cells to become increasingly segregated. Cities in the US, in particular, had been experiencing the physical segregation of cities by race, with the assumption being that such spatial divisions were the result of strong biases amongst residents. With his model, Shelling demonstrated that, in effect, total segregation could occur even when agent 'rules' were only slightly biased towards maintaining neighborhood homogeneity. While the model does not explain why spatial segregation occurs in real-world settings, it does shed light on the idea that strong racial preferences are not, by necessity, the only reason why spatial partitioning may occur.
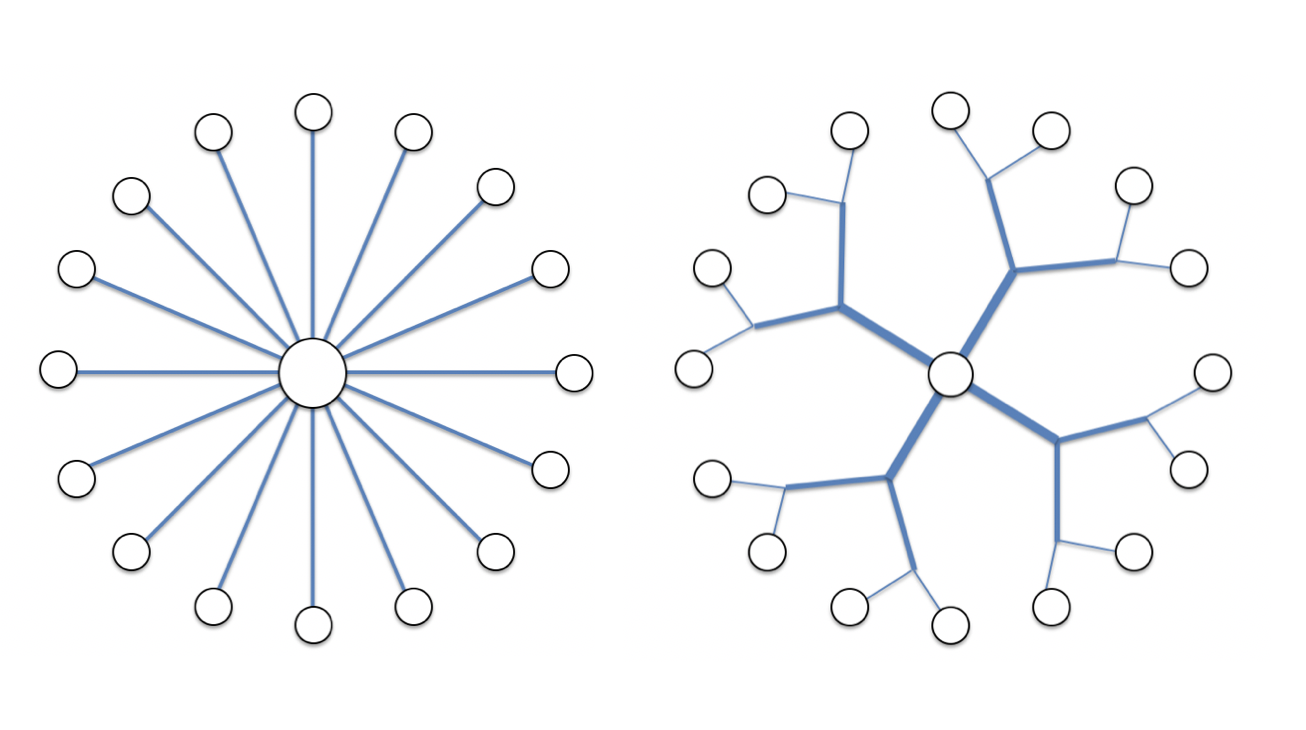
Because of the implicitly spatial qualities of models like Conway's and Shelling's, both computer programmers and urban thinkers began to wonder if models might help explain the kinds of spatial and formal patterns seen in urban development. If so, then by testing different rule sets one might be able to predict how iterative, distributed (or bottom-up) decision-making ultimately affects city form.
This is a unique direction for planning, in that most urban strategies focus on generating broad, top-down master-plans, where the details are ultimately filled in at a lower level. Here, the strategy is inverted. Models place decision-making at the level of the individual cell in a lattice, and it is through interacting populations of these cells that some form of organization is achieved. Models were able to demonstrate that, depending on the nature of the interaction rules, the formal characteristics of this emergent order can differ dramatically.
Ultimately, by running multiple models, and observing what kinds of rule-sets generate particular, recurrent kinds of pattern and form, modelers are able to speculate on what policy-decisions around planning are most likely to achieve forms deemed 'desirable' (on the assumption that the models are capturing the most salient feature of the real world conditions, which is not always the easiest assumption to make!).
Agent Based Models
Cellular Automata simulations are formulated within a lattice-type framework, but clearly this has its limits. The assumption of the model is that populations of cells within the lattice have inter-changeable rule sets, and that emergent features are derived from interactions amongst these identical populations. Clearly the range of players within a real-world urban context are quite variable, and populations of uniformly behaving cells do not capture this variance. Accordingly, with the growth in computing power, a new kind of "agent-based model" was able to liberate cells (or agents) from their lattices, as well as enabling programmers to provide differing rule-sets for multiple, differing agents.
In such models, we might have two sets of agents, (predator/prey), or agents moving in a non-static environments (flocking birds/schools of fish). Simple rules sets are then tested and calibrated to see if behaviors emerge within the models that emulate real-world observations. These models then demonstrate how different populations of actors or 'agents' with differing goals and rule sets interact.
Models that are straightforward to code (Net Logo is a good example, which can be deployed either as a CA or an Agent-Based model), showcase how different populations/agents within a model interact, producing unexpected results. Rules of interaction can be easily varied, according to a limited number of defined parameters.
That said, depending on how variables are calibrated, very different kinds of global behaviors or patterns emerge.
Urban Applications:
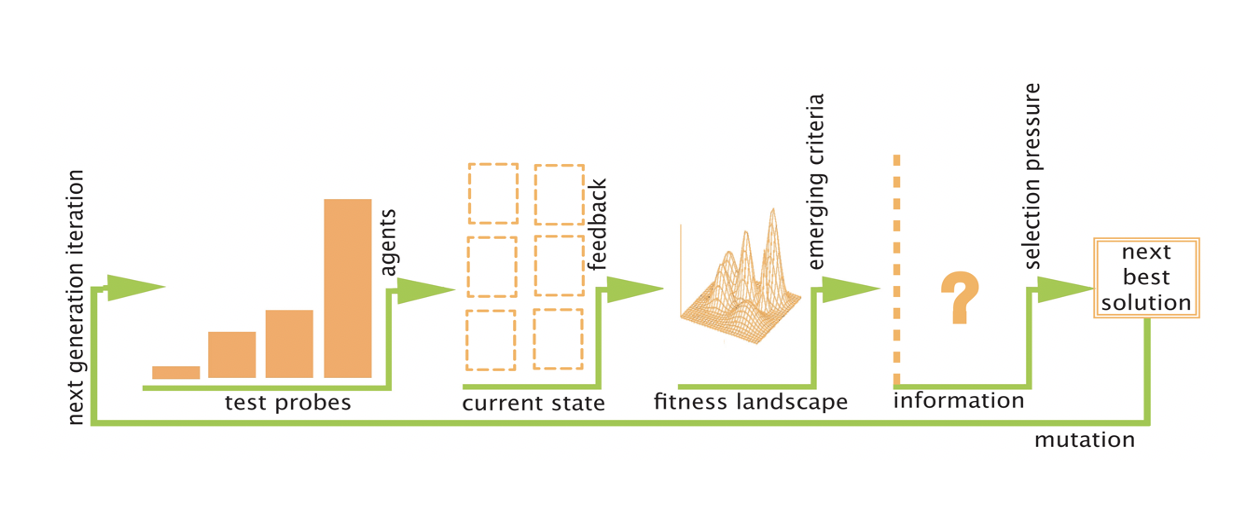
All of this is of great interest to urban computational geographers, who attempt to employ computer models as stand-ins for real world situations. From an urban standpoint, an agent might be a resident, a business owner, a shop-keeper, etc. Depending on the rules for growth, purchase pricing, development restrictions, or formal (physical) attributes, these agents can be programmed to interact upon an urban field, with multiple urban simulations (that use the same rule sets), serving to probe the 'field of possibilities' to see if any regularities emerge across different scenarios or iterations. If such patterns are observed, then the rules can be altered - in an attempt to derive which rule characteristics are the most salient in terms of generating either favorable or unfavorable spatial conditions (again, with the proviso that the interpretation of 'favorability' might well be contested).
Such models, for example, might attempt to show the impact of a new roadway on traffic patterns, with various rules around time, destination, starting position, etc. By running various tests of road locations, a modeler might attempt to determine the 'best' location for a new road - with the 'fitness' of this selection tying in to pre-determined policy parameters, such as land costs associated with location, reduction of congestion/travel times, or other factors. The promise of these models is very powerful: to simulate real-world conditions within a computer and then build multiple test 'worlds' prior to real-life implementation. This allows modelers to minimize policy risk of unknown consequences that are teased out in simulations.
Inherent Risks
That said, in practice there is always the concern of what models do not include: are the assumptions of the model in fact in alignment with the real world? To alleviate this, modelers attempt to calibrate their models to real world conditions by using data sets wherever possible, but they remain limited by which data types are available to them. Furthermore, the fact that a given data-set is available for use/calibration purposes, does not necessarily mean that the features the data captures are in fact related to the most salient indicators or features of the real-world system.
Models, can often be seen as 'objective' or 'scientific', since once the code has been written, the models provide reliable, quantitative results, but this does not mean that the consistency of the model is consistent with the real-world conditions being model. The model is still subject to the biases of the coding, the decisions of the modeler, and ideas around what to include and what to disregard as unimportant.
In an effort to include more and more potential factors (and again, with rising computer power) agent-based models have become increasingly sophisticated, integrating additional real-world conditions. However, as the models grow to contain more and more conditions, actors, and rules, their relationship to complex adaptive systems perspectives has become increasingly tenuous. Scientists originally interested in the dynamics of complex systems were struck by the fact that simple systems with simple rules could generate complex orders. It should not, however, be surprising that complex models, with increasingly complex rule sets can generate complex orders, but the effort going into the creation of such models, their calibration, and their interpretation (in terms of how they guide policy), seems to have moved increasingly far away from the underpinnings of their inspiration.
What seems to have been preserved from complexity theory - rather than the simplicity of complex systems dynamics - are three ideas: that of "bottom-up" rather than top-down logic - whereby the order of the system emerges without need for top down control, and the idea of "emergence": that interacting agents within the model can generate novel global patterns or behaviors that have not been explicitly programmed into the system. Finally, at the individual agent level, the rules can still retain a simplicity.
While many individual researchers and research clusters investigate urban form through modeling, it is worth making special note of CASA - The Center for Advanced Spatial Analysis at the Bartlett in London, a group led by Professor Mike Batty.
Model Attributes: Fractals and Power Laws
Of interest to Urban Modelers is not just the emergent patterns found in simulations, but also the ways in which these patterns correspond to features associated with complex systems. For example, many models display {{fractals-1}} qualities. The illustration below (taken from an article by Mike Batty) show variants of how CA rules generate settlement decisions, with fractal patterns emerging in each case. Different initial conditions/constraints yield different kinds of fractal behavior (except in starting condition B).

Example of Emergent Fractal spatial characteristics, 'A digital breeder for designing cities' (2009)
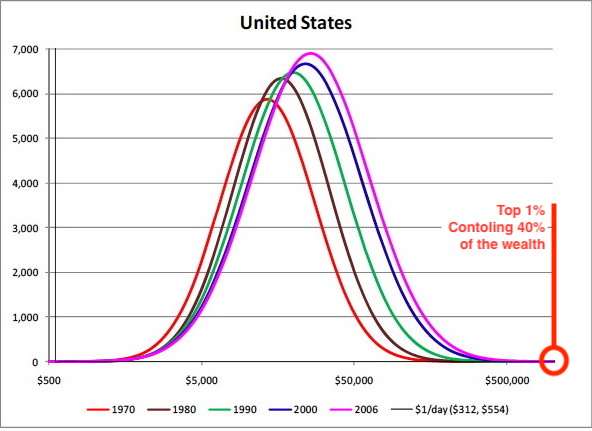
Similarly, models often exhibit {{power-laws}} in their emergent characteristics - whether this be factors such as population distributions of cities in a model, or distributions of various physical attributes within a given city. For example, an analysis of internal city road networks might reveal that road use frequency in a given city follows a power-law distribution; another analysis might reveal that cities within a given country can be ordered by size, and that populations between cities follow a power law distribution (this characteristic seems to hold for cities that together form part of a relatively interdependent network - for example the grouping of all cities in the USA, or France, but not groupings of all cities in the world, suggesting that these are not part of the same system).
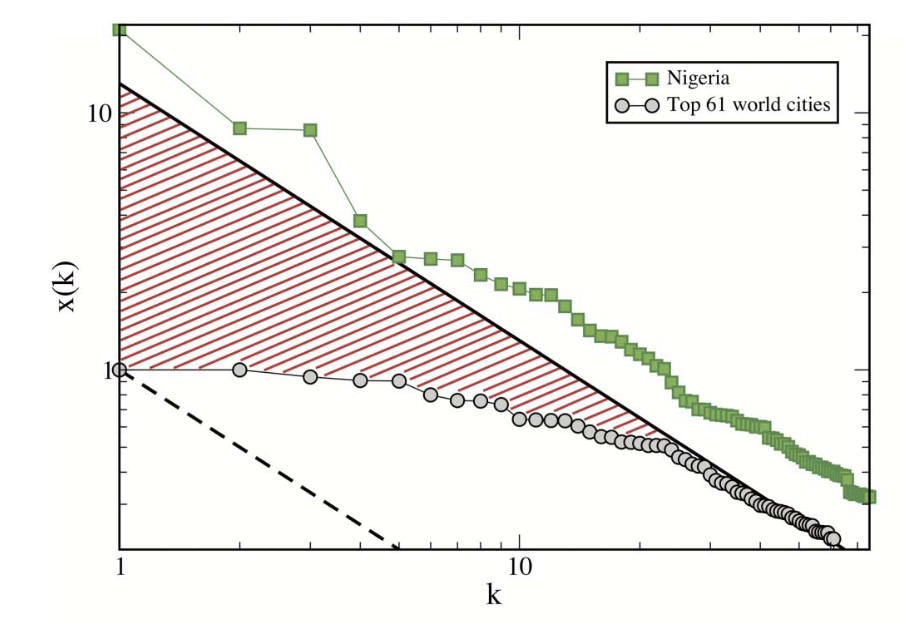
Example of power-law distribution of city populations in Nigeria, which closely follow Zipf's law: Image from Scientific Report "There is More than a Power Law in Zipf" by Cristelli, Batty and Pietronero (2012)
Many academic papers from the urban modeling world stress these attributes, which are not planned for and which are often characterized as being the 'fingerprint of complexity'.
Model Dynamics: Tipping Points & Contingency
Alongside these observed attributes of models - power laws and fractals - modelers are also interested in how models unfold over time. One of the interesting aspects of models is that, while the overall characteristics of emergent features might be similar across different models, the specificity of these characteristics will vary.
For example, a model might wish to consider locational choices of individual within a region, and including populations of agents that include such categories as: 'job opportunities', 'job seekers', and 'land rent rates'. In such a scenario, what begins as a neutral lattice of agent populations will ultimately begin to partition and differentiate with varying areas of population intensity (cities, towns) emerging. The size of these various populations centers might then follow a power-law. If we repeat the simulation with the same rules in place, we would expect to see similar power-law population patterns emerge, but the specificity of exactly where these centers are located is contingent - varying from simulation to simulation.
This raises the question of the true nature of cities and population dynamics: for example, the fact that Chicago is a larger urban hub than St. Louis might be taken as a given - the result of some 'natural' advantage that St Louis does not have. But model simulations might suggest otherwise - that the emergence of Chicago as the major mid-west hub is a contingent, emergent phenomena: and that history could have played out differently.
Models therefore allow geographers to understand alternative histories, and consider how what might seems like a 'natural' outcome, seen as part of a clear causal chain, are in fact much more tenuous and contingent phenomena. Had the rules playing out just a little differently, from a slightly different starting point, a completely different result might have ensured. Here, we are left with the realization that {{history}}, and that {{contingency}} plays a key role in the make-up of our lived world.
Another way this can be thought of is the idea of a Tipping Points: that whether or not Chicago or St Louis became a major urban center was the result of a small variable that pushed the system towards one regime, whereas another, but completely different regime was equally viable.
Tipping Points are discussed elsewhere on this site, but it is important to state that they can be thought of in two different ways: the first is this idea of a minor fluctuation that launches a given system along one particular path versus another, due to reinforcing feedback. The second looks at how an incremental increase in the stress or input to a system, once moved beyond a certain threshold, can push a system into an entirely new form of behavior.
This second idea becomes important in modeling the amount of stress or inputs a given urban system can tolerate (or absorb) before one behavioral regime shifts to another. For example incrementally rising fuel prices might reach a point where people opt to take public transit. Or a certain critical mass of successful business ventures might eventually result in a new neighborhood hub, at which point rents increase substantially. What is interesting about these points is that the shift is often abrupt, as people recalibrate their expectations and behaviors around a new set of parameters that have exceeded a particular threshold. Models can display these abrupt shifts, or Phase Transitions, where certain patterns disappear only to be replaced by others.
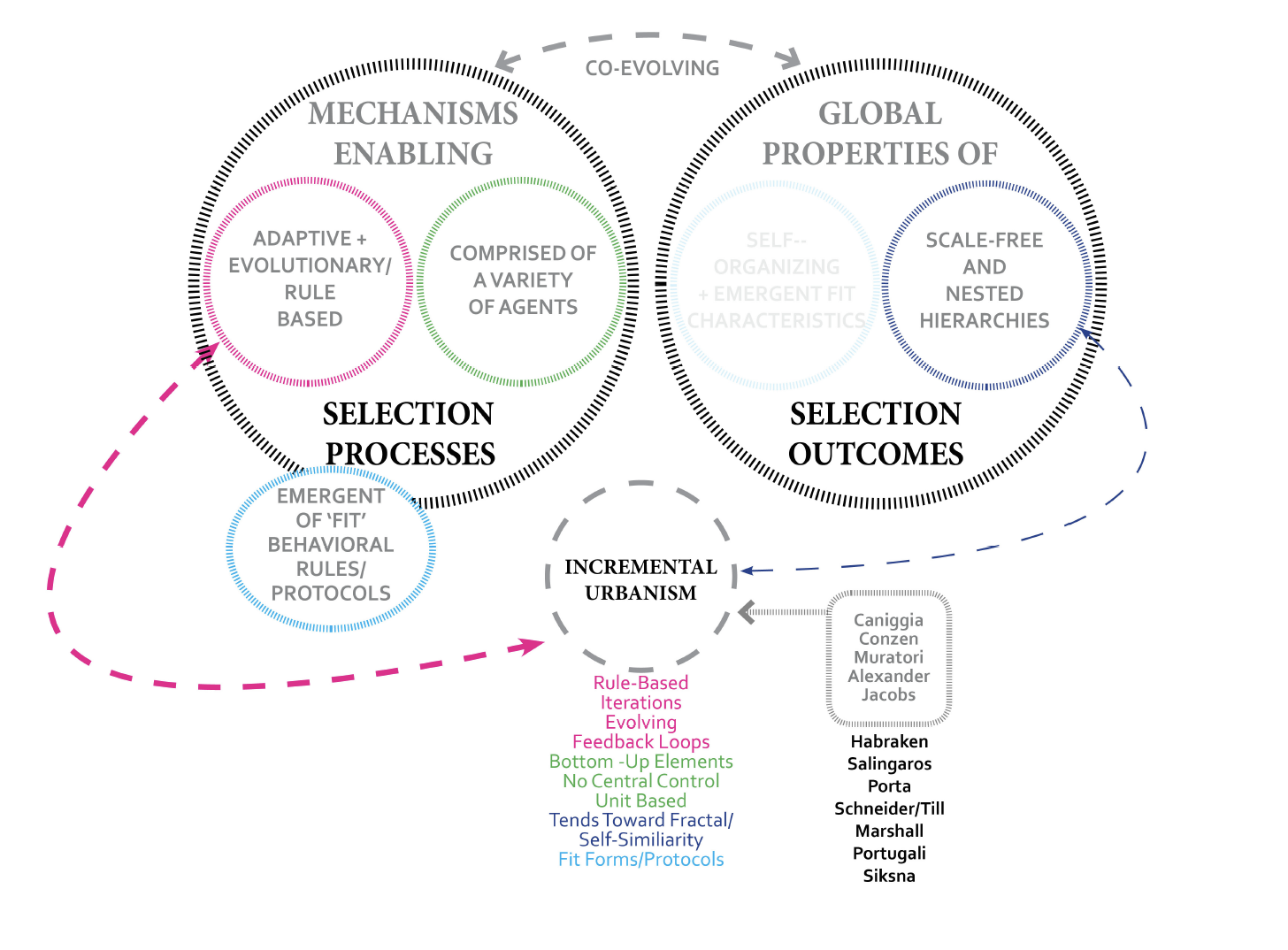
A sketch outlining some of the ideas and individuals associated with urban modeling
Back to {{urbanism}}
Back to {{complexity}}