Tipping Points

Most of us are familiar with the phrase 'tipping point'. We tend to associate it with moments of no return: when overfishing crosses a threshold that causes fish stocks to collapse or when social unrest reaches a breaking point resulting in riot or revolution. The concept is often associated with an extreme shift, brought about by what seems to be a slight variance in what had been incremental change. A system that seemed stable is pushed until it reaches a breaking point, at which point a small additional push results in a dramatic shift in outcomes.

Example:

Water molecules respond to two critical points: zero degrees, when they shifts from fluid to solid state; and one hundred degrees, when they shift from fluid to vapor state. We see that the kinds of behavior that water molecules will obey is context dependent:  they maintain fluid behaviors within, and only within, the context of a certain temperature range. If we examine why the behavior of the water changes, we realize that fluid behavior within the zero to 100 range is the behavior that involves the least possible energy expenditure on the part of the water molecules given their environmental context. Once this context shifts - becoming too cold or too hot - a particular behavioral mode is no longer that which best conserves energy. Water molecules have the capacity to enact three different kinds of behavioral modes - frozen, fluid, or vapor - and the way these modes come to be enacted is subject to whichever mode involved the least energy expenditure within a given context.

Minimizing Processes:

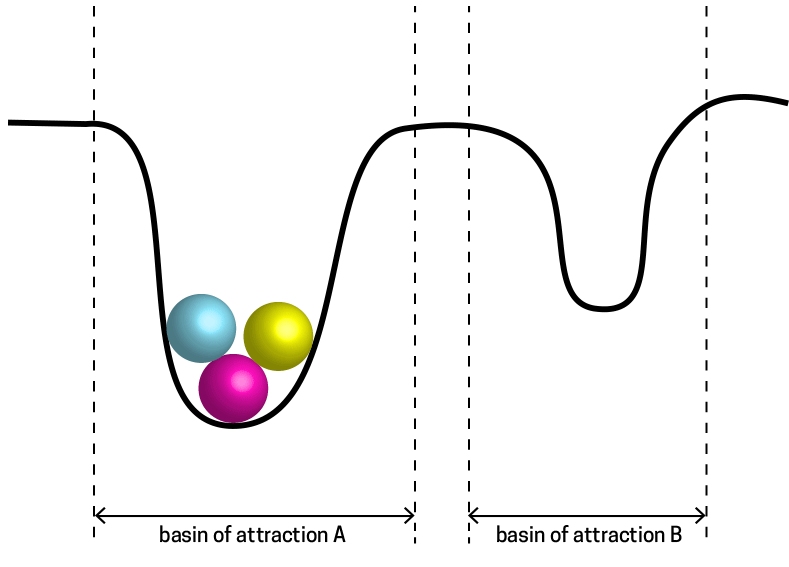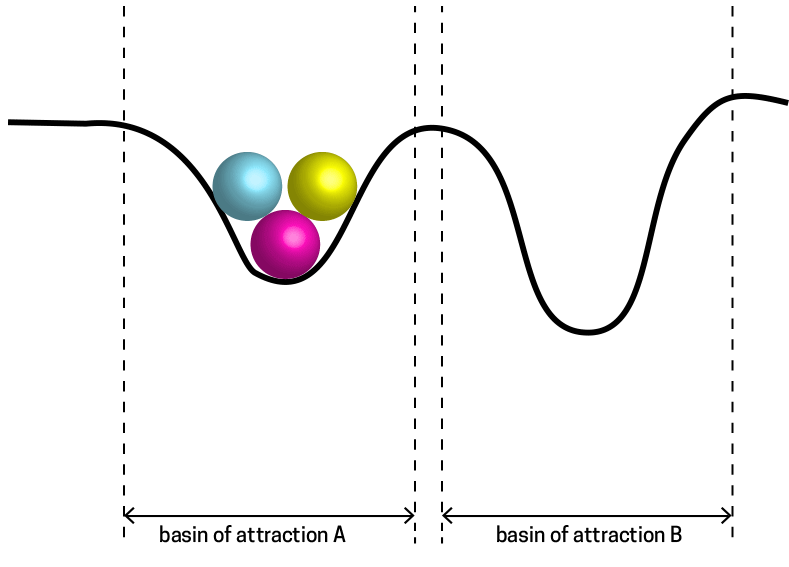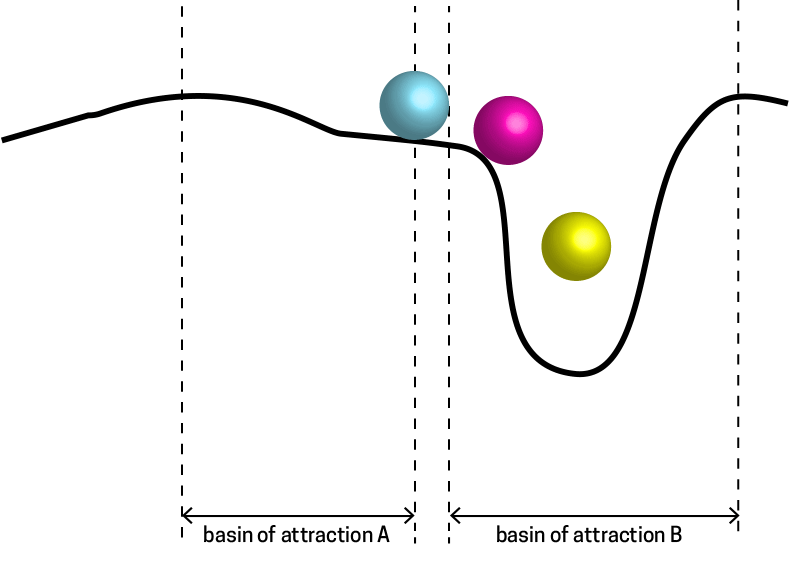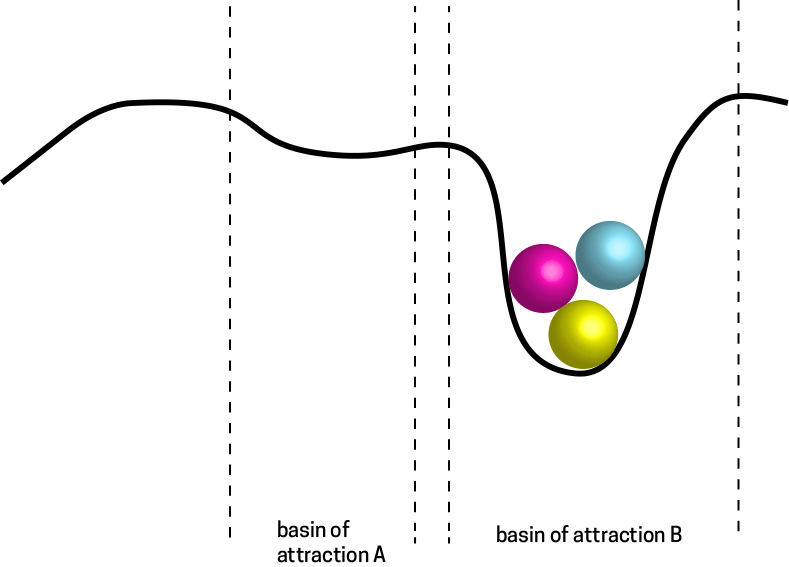
Another way to think about this, using a complex systems perspective, is that the global behavioral dynamics are moving from one Attractor States to another. When the context changes, the water molecules are forced into a different "basin of attraction" (another word for an attractor state), and this triggers a switch in their mode.

In all complex systems this switch from one basin of attraction to another is simply the result of a system moving from a regime of behavior that, up until a certain point, involved a minimized energy expenditure. Beyond that point (the tipping point) another kind of behavioral regime encounters less resistance, conserving energy expenditures given a shifting context.

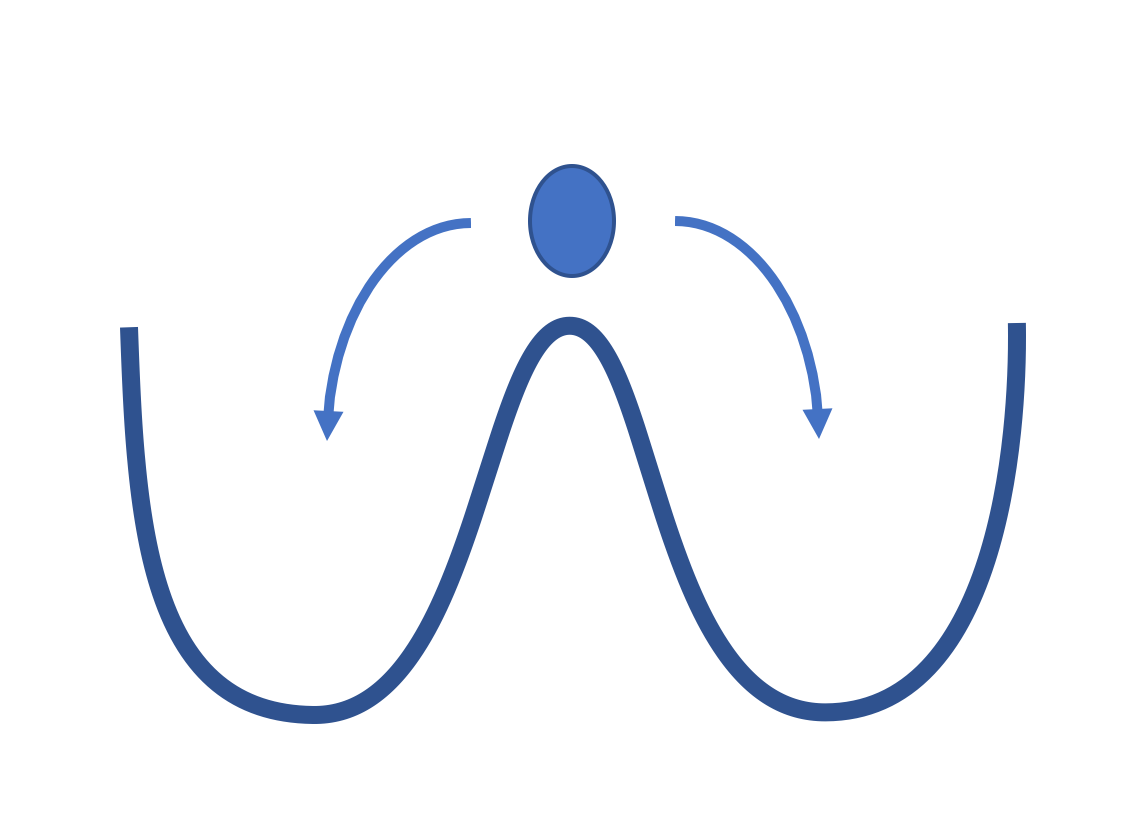
A tipping point, or critical point is one where a system moves from one regime of 'fit' behavior into another. We can imagine the point above as a water molecule poised at zero degrees - with the capacity to manifest either in a fluid or frozen energy state.

Of course, what we mean by 'conserving energy' is highly context-dependent. For example, even though the individual members of a political uprising are very different actors from individual water molecules in a fluid medium, the dynamics at play are in fact very similar. Up until a certain critical mass is obtained, resisting a government or a policy involves encountering a great deal of resistance. The effort might feel futile - 'a waste of energy'. But when a movement begins to gain momentum, there can be a sense that the force of the movement is stronger than the institutions that it opposes. Being 'carried along' with the movement (joining an uprising), is in fact the course of action that is most in alignment with the forces being unleashed.

Further, once a critical mass is reached, a movement will tend to accelerate its pace due to positive feedback. This can have both positive and negative societal consequences: some mass movement such as lynching mobs or bank-runs show us the downside of tipping points that move beyond a threshold and then spiral out of control.

That said, understanding that critical points may exist in the system (beyond which new kinds of behavior become feasible), can help us move outside of 'ruts' or 'taken for granted' scenarios. In the North American context, smoking was an acceptable social practice in public space. Over time, societal norms pushed public smoking beyond a threshold of acceptability, at which point smoking went from being a normative behavior to something that, while tolerated, is ostracized in the public realm.

What other kinds of activities might we wish to encourage and discourage? If we realize that a behavioral norm is close to a critical point, then perhaps with minimal effort we can provide that additional 'push' that moves it over the edge.

Shifting Environmental Context:

Of course these examples are somewhat metaphoric in nature, but the point being made is that there can be changes in physical dynamics and changes in cultural dynamics that cause different kinds of behaviors to become more (or less) viable within the constraints of the surrounding context.

Returning to physical systems, slime mould is a very unique organism that has the capacity to operate either as a collective unit, or as a collection of individual cells, depending on the inputs provided by the environmental context. As long as food sources are readily available, the mould operates as single cells. That said, when food becomes scarce, a critical point is reached when cells agglomerate to form a collective body with differentiated functions. This new body has capacities for movement and food detection not available at the individual cell level, as well as other kinds of reproductive capacities.

Accordingly, we cannot think about the behavior of a complex system without considering the context within which it is embedded. The system may have the different kinds of capacities depending on how the environment interacts with and 'triggers' the system. It is therefore important to be very aware of the environmental coupling of a system. What might appear to be stable behavior might in fact be behavior that is relying on certain environmental features being present - change these features and entirely new kinds of behaviors might manifest.

This is to say that tipping points might be extended both from intrinsic forces and extrinsic forces (also termed endogenous vs exogenus aspects). This is to say that a shift might be due to dynamics at play within the system, that push it beyond a critical threshold, or they may be due to dynamics external to the system, that alter the system context or inputs in such a way that a system's particular behavior can no longer be maintained and is pushed into a new regime. When the forces are external, we can think of this as shifts to the Fitness Landscape, where a particular mode of operation is no longer viable due to differences in the environmental context.

Back to Core Concepts

Back to Navigating Complexity