Bifurcations

The term Bifurcation is used in complexity theory in three subtly different ways. The first relates to a split or 'choice' between two equally viable states (or Attractor States),  as in Benard Roll experiments when heated liquid forms 'roll' patterns that can either roll left or roll right. The ‘choice’ of which of these states will manifest is not predictable, as the system is highly  Sensitive to Initial Conditions, with small changes in these potentially leading to large shifts in the system’s ultimate global behavior.  This kind of Bifurcation is perhaps best captured colloquially by the phrase  Tipping Points, (as popularized by Malcolm Gladwell) - and relates to moments when a system has the capacity to move into two equally viable alternative regimes. 

The second use of the term is invoked when a system behavior suddenly acquires new features, such as when water molecules turn to ice at a particular temperature. This is thought of as a bifurcation, since the heating or cooling at that temperature point will cause the system to manifest with one set of features, (liquid) versus another set of features (solid). We see that this is similar to the first way in which we speak of bifurcations, in that the system is still sensitive, and it is poised between two different sets of stable behaviors. The difference is in the first instance (rolling left or right), the two system states are not qualitatively different.  In this second usage of bifurcation, the difference is a much more extreme qualitative difference, such that the system is hardly recognizable as being composed of the same entities. These shifts can also be considered as tipping points, but due to the dramatic shifts in behavior they are probably best described as 'catastrophes' a term dubbed  by René Thom, to describe these threshold moments. Reimann Manifolds offer a way to visualize these catastrophes, while also framing these moments within a broader Phase Space of possible systems states. The manifolds illustrate how systems can move smoothly through multiple potential states and then shift suddenly at these critical points.

The third use of the term is reserved for a particular kind of system that can cycle between different attractor states, with the number and nature of these cycles varying according to the strength of a particular input.  These systems are described on what are called either "Bifurcation diagrams" or "Logistic Maps". These diagrams are applicable in a range of systems, all of which involve systems that are simultaneously subject to  a particular amplifying force (called a control parameter)  that left unchecked results in Positive Feedback.  Simultaneously the systems are constrained by a more constant, dampening force of Negative Feedback. When these two forces are out of sync (the rate of amplification cannot be steadily repressed by the negative feedback, the system will begin to demonstrate changes in behavior at particular thresholds of the control parameter force.  At these moments, the system will shift from a regime where it is growing steadily, to one where it begins to oscillate between growth and decline (booms and busts). If the amplification rate, is increased even more, the oscillation will begin to move between cycles ever more erratically: first cycling amongst 4 behaviors, then 8, 16, and so forth. As the control parameter increases, the number of system states multiplies exponentially (with strange windows of calm where the counter-acting rhythms seems to snap the behavior back towards more orderly cycles involving 3 states). That said,  eventually the system will arrive at a ‘chaotic’ regime wherein all potential states are accessible. 

In this third example, every point at which the system begins to shift so that it moves into a different cycle of rhythms is considered to be a bifurcation point.  That said the system is not "choosing" between states (as we had in earlier examples), but instead iteratively cycling between states. Furthermore, the bifurcation is not so much about the cycling, but is instead about moments in the system when cycling moves from one rate to another rate (becoming steadier if the amplifying parameter is decreased, and more erratic if it is increased).

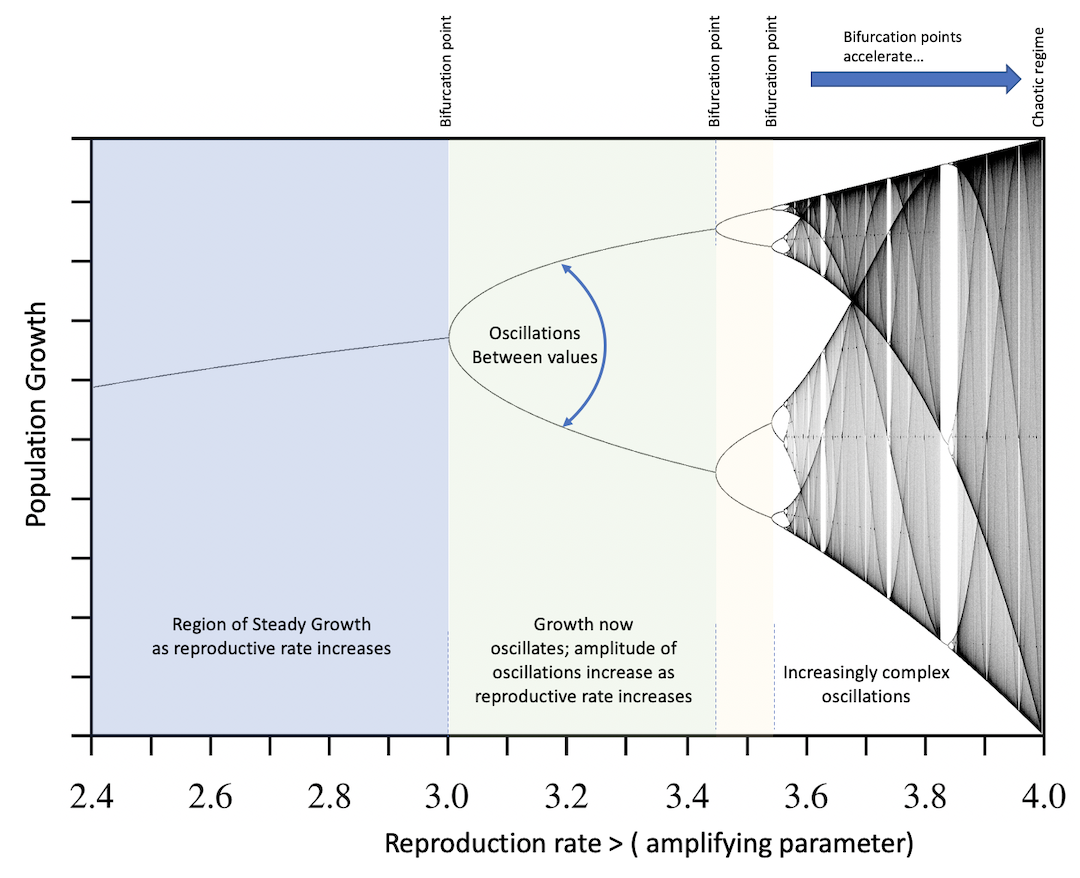
The classic example of Logistic Map is its use to describe the behavior or a reproducing animal in a finite eco-system. This derivation was first produced by Robert May, to show how a population with a particular reproduction rate that is gradually increased (the amplifying control parameter), will ultimately display seeming erratic behavior. When the reproduction rate is low,  small increases in the rate of reproduction create steady but low population growth.   At a given moment, when the suppression feedback of the carrying capacity of the ecosystem can no longer support the additional population members,  the system will begin to cycle (booms and busts in the population rates). This cycling will remain constant as long as the reproduction rate holds steady. That said if it increases, the nature of this cycling becomes ever more irregular.

Folded into this diagram are a number of interesting features, including the presence of power-law regularities that have been identified by  Mitchell Feigenbaum. 

The most amazing diagram!
While this is the most famous example of the bifurcation diagram, other systems follow parallel dynamics, and can be diagrammed using the same map. Rates of dripping water (force of flow being the amplifying parameter, water drop surface tension being the dampening or restricting force, will obey the identical sequence.

It may be that any system governed by competing and unequal forces of  expansion/ constraint;  push/pull; or positive; negative feedback will exhibit these same regularities. That said, the two competing forces need to be coupled in some way - such that the driving feedback of one (population growth), increasingly activates the driving feedback of the other (limited carrying capacity), in ways that are coupled. 

It is currently unknown how many systems follow the kinds of behaviors described in the bifurcation map, but it has cropped up in some unusual places, including in fractals. The video below is probably the best exposition of bifurcation tree behavior that is around.