Degrees of Freedom

The notion of degrees of freedom comes to us from physics and statistics, where it describes the number of possible states a system can occupy. For example, a swinging pendulum is constrained to a fixed number of 'states' (positions in space) that the pendulum can occupy. We can imagine that it is possible to map out all the potential locations of the pendulum's swing, and therefore the limits of all it behaviors. The degrees of freedom thus tells us something about what a system is capable of doing: it's potential. The system cannot act outside of the boundaries of this action potential.

For example, if we wanted to examine the maximum capacity of motion for a three-dimensional object in space, this can be provided using just six degrees of freedom, which together define changes both in orientation: (rotation) that occurs via the 'roll', 'yaw' and 'pitch' motions; and for changes related to displacement in space: through the 'up/down', 'back/forward' and 'left/right' parameters. We can see that all potentialities of movement are covered within this framework.

If we were to eliminate any of these parameters - for example the 'up/down' potential, then we have fewer degrees of freedom, certain types of movement would no longer be possible. Phase Space - thereby captures the sum total of all potential behaviors - sometimes referred to as a system's 'possibility space'.

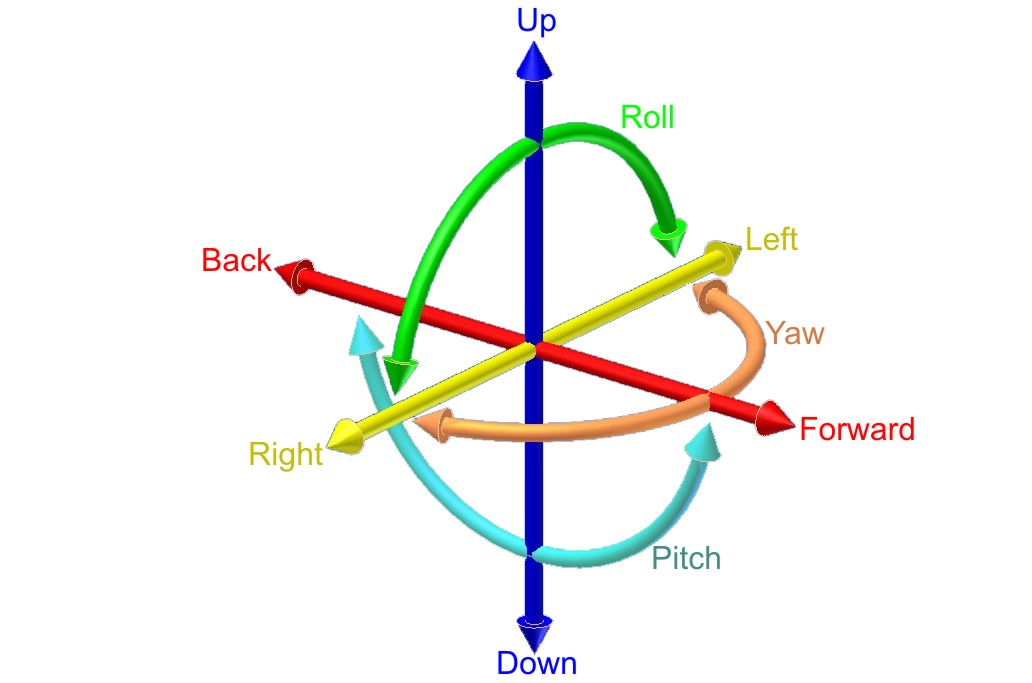
(image courtesy of Wikimedia commons)

In addition to there being a range of phase space potentials, there may also be particular behaviors in phase space that are more likely to occur. Accordingly, if we were to map all of the potential states of a pendulum's behavior from any given starting position in phase space, we  would have what is known as a 'phase portrait' of that pendulum. This is to say that there are particular trajectories that the pendulum will follow within phase space. Different systems might have phase portraits that highlight certain special regions of phase space as being Attractor States which a system will tend to gravitate towards.

Human Systems

So far we have been speaking about physical degrees of freedom, but we might also imagine degrees of freedom in relation to behavioral possibilities.

Example:

Imagine we are wanting to stay at an airbnb. We could think of each airbnb option as being an agent in a complex system, competing to win us over by broadcasting its 'fitness' for our stay. Each Airbnb would be able to adjust a number of parameters that one might consider as important in choosing accommodation. These parameters could include cost, cleanliness, distance to center, size, and quietness. Different people might value (or weigh) these parameters differently, and choose their airbnb accordingly. At the same time, we can imagine that each airbnb has a capacity to adjust its 'state' to different degrees. Location is clearly a limited parameter: a given airbnb has no capacity to simply change its location. But it does have the capacity to adjust its price point. Size is also difficult to alter. But cleanliness might have more flexibility. Thus certain categories have more range in terms of their degrees of freedom than others. If airbnbs are considered as agents in a complex system, each competing to find patrons who wish to stay at their location, then they each have to operate within their particular bounds of freedom in terms of how they adjust to align themselves better with user needs. Thus if they can't compete on the basis of location then they can attempt to compete on the basis of cost.

More Than Three Dimensions - No Problem!

The airbnb case should also serve to illustrate that, in many scenarios, the degrees of freedom available to an agent in a complex system cannot be easily plotted in three dimensional space (that is a 'space' bounded by an x, y, and z axis). That said, just because phase space cannot always be easily visualized in three-dimensional space, it doesn't mean we have to bend our minds to imagine more than 3 degrees of freedom. Just because we can't easily draw a graph of all these potential parameters, we can certainly imagine sorting different priorities simply as parameter bars with weights. We then have a multi-parameter space that the agent is calibrated within.

Multiple Degrees of Freedom thought of as sliding parameter bars: 

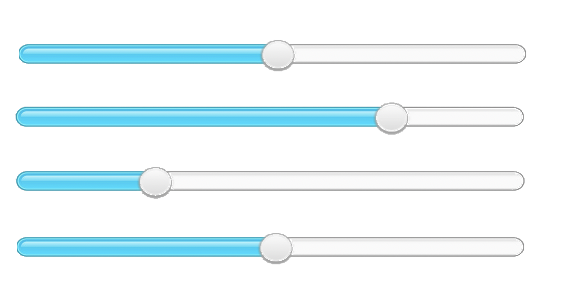
Requisite Variety

Analyzing  agents in complex system according to their Degrees of freedom can thus be thought about as examining their range of possible parameter settings. This can be an extremely helpful way of thinking about the {{adaptive-capacity}} of the system: or what it can and cannot do in response to environmental changes or fluctuations. Another way to describe this is the idea of a system's Requisite Variety: a phrase coined by Ross Ashby to highlight the amount of variability a system can enact. According to Ashby, a system needs to have a variety of responses commensurate with the variety of inputs. This responsive capacity can be defined more precisely by means of defining the agent's degrees of freedoms. 

Back to Core Concepts

Back to Navigating Complexity